Benchmarking and scalability¶
DFTB+ has an internal timer for various significant parts of its calculations. This can be enabled by adding the following option to the input:
Options {
TimingVerbosity = 2
}
This will activate the timers for the most significant stages of a calculation. Higher values increase the verbosity of timing, while a value of -1 activates all available timers.
The typical output of running the code with timers enabled for a serial calculation will end with lines that look something like
--------------------------------------------------------------------------------
DFTB+ running times cpu [s] wall clock [s]
--------------------------------------------------------------------------------
Pre-SCC initialisation + 3.46 ( 5.8%) 3.45 ( 5.8%)
SCC + 47.34 ( 79.6%) 47.34 ( 79.6%)
Diagonalisation 44.79 ( 75.3%) 44.79 ( 75.3%)
Density matrix creation 2.21 ( 3.7%) 2.21 ( 3.7%)
Post-SCC processing + 8.68 ( 14.6%) 8.68 ( 14.6%)
Energy-density matrix creation 0.55 ( 0.9%) 0.55 ( 0.9%)
Force calculation 7.74 ( 13.0%) 7.74 ( 13.0%)
Stress calculation 0.94 ( 1.6%) 0.94 ( 1.6%)
--------------------------------------------------------------------------------
Missing + 0.00 ( 0.0%) 0.00 ( 0.0%)
Total = 59.48 (100.0%) 59.47 (100.0%)
--------------------------------------------------------------------------------
This shows the computing time (cpu) and real time (wall clock) times of major parts of the calculation.
An alternative method to obtain total times is by using the built-in shell command time when running the DFTB+ binary
time dftb+ > output
In the above example, at the termination of the code timings will be printed:
real 0m59.518s
user 0m59.430s
sys 0m0.092s
More advanced timing is possible by using profiling tools such as gprof.
Examples¶
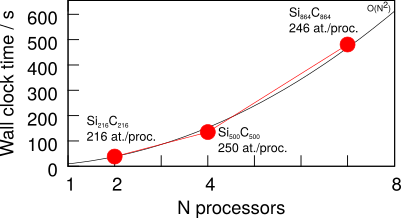
Distributed memory parallelism¶
This section coming soon!
Topics to be discussed:
- Parallel scaling of simple examples.
- Parallel efficiency.
- Use of the Groups keyword in DFTB+ to improve scaling and efficiency for calculations with spin polarisation and/or k-points.
- Effects of latency on code performance.