Amdahl’s law¶
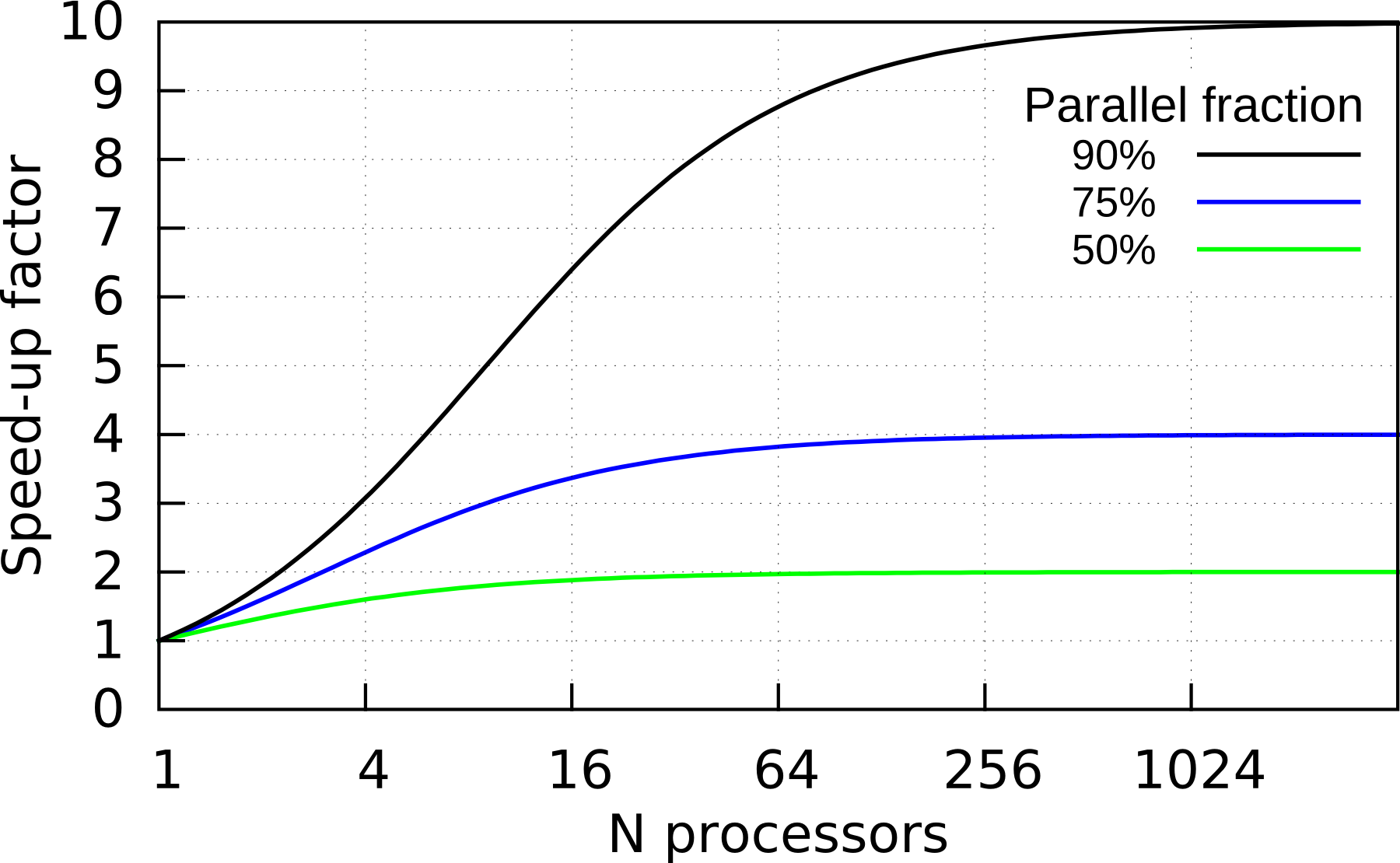
One of the major issues in the performance of a parallel program is the possible speed up from using parallelism. Amdahl’s law describes the expected gains for operations which are partially parallelised, i.e., where there are computational parts that must be performed in serial as well others which operate in parallel. If the fraction of the operations performed in parallel are p, then compared to serial operation, the expected speed-up is:
Amdahl’s law can provide a reasonable indication of the performance of a problem on increasing numbers of processors, depending on the parallelism of the task:
As you can see, only substantially parallel tasks give substantial speed up on larger numbers of processors. The limiting speed up for large numbers of processors is
i.e., the inverse of the serial fraction of the code, which gains nothing from parallelism.
Amdahl’s does not include the effects of latency or the cache hierarchy on parallel performance, but can be a good guide to the limits of scalability for fixed sizes of problem on parallel machines.
Gustafson’s law¶
Amdahl’s law assumes that the size of the computational problem remains fixed as the number of processes increases. However, it is often more common that the problem is increased along with the number of processes.
This situation is partly described by Gustafson’s law. However in the case of DFTB the computational effort for conventional diagonalisation (the dominant part for most calculations) grows as the cube of the number of atoms. This complicates the situation. In principle idealised weak scaling where the number of atoms increases proportional to the number of processors would give a time to solution that grows as the square of the number of atoms.
See for example Snyder, Annu. Rev. Comput. Sci. 1: 289, 1986 for a discussion of these issues.