Ehrenfest dynamics¶
As explained above (in the introduction to the Electronic dynamics chapter) electron-nuclear dynamics within the Ehrenfest ansatz are based on the integration of the ionic equations of motion using the expectation value of the force that corresponds to the current density matrix. Nuclear dynamics drive electronic dynamics in turn through the time-dependent nuclear positions that appear in the Hamiltonian. The nuclear and electronic systems interact through expectation values and therefore Ehrenfest is a mean-field approximation to the actual coupled electron-ion dynamics. This approximation is useful in some situations; however, the neglected electron-ion correlations might be essential for some processes. The crossing of conical intersections, for example, is where the approximation breaks down drastically.
Benzene example¶
[Input: recipes/electronicdynamics/ehrenfest/]
As an example of Ehrenfest dynamics, starting from the equilibrium geometry we
can excite the lowest-lying \(\pi-\pi^*\) excitation of a benzene molecule
using a short laser pulse, and explicitly allow the ions to move. In this case,
the ElectronDynamics blocks is as follows:
ElectronDynamics = {
Steps = 100000
TimeStep [au] = 0.1
Perturbation = Laser {
PolarizationDirection = 0.00000001 0.61419463 -0.78915459
LaserEnergy [eV] = 6.834 # pi-pi* transition energy
}
EnvelopeShape = Sin2 {
Time1 [fs] = 10.0 # end-time of the pulse
}
FieldStrength [V/A] = 0.10
IonDynamics = Yes
InitialTemperature [K] = 0.0
Populations = Yes
}
The keyword IonDynamics is set to Yes and for this example, we are
starting with zero initial atomic velocities. The short, but strong, laser pulse
drives electrons from the HOMO to the LUMO and this sudden change in the
electronic structure impulsively drives the nuclei to move. In the following
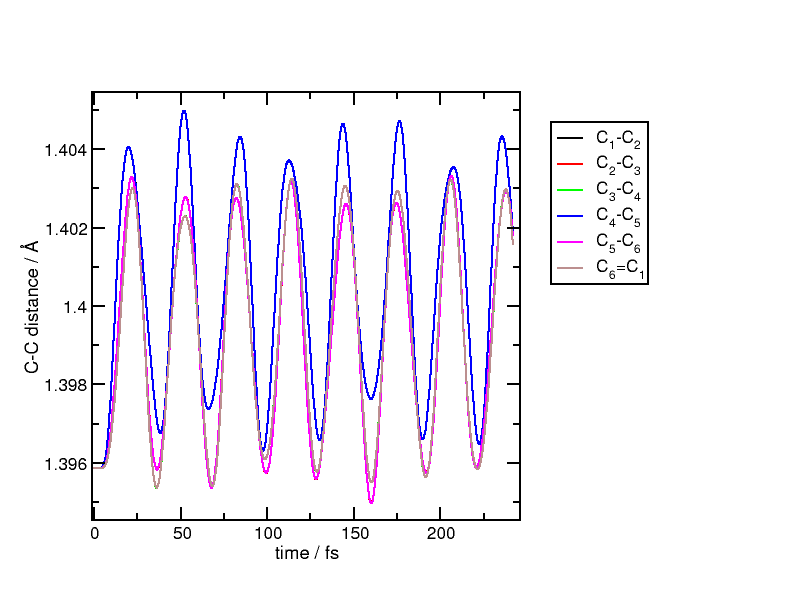
figure, we plot the distances between neighbouring carbon atoms in the benzene
ring:
After the short excitation, all carbon atoms move in a breathing motion with all distances increasing and decreasing periodically. The breathing is not perfect but is a good approximation of the actual motion. The process can be explained if we picture the state of the system being in a coherent superposition between the ground and excited states. In this superposition, electrons which were occupying bonding orbitals now partially populate anti-bonding orbitals. In this highly symmetric molecule, all C-C bonds lose strength and therefore, after the excitation, the equilibrium position is displaced to a longer inter-atomic distance. This sudden change of effective potential energy surface drives the nuclear motion, which now oscillates around the new displaced equilibrium.